Hydromagnetic Boundary Layer Flow and Heat Migration of Dual Stratified Eyring-Powell Fluid

Simon Waswa Wekesa; Winfred Nduku Mutuku

doi:doi:10.11648/j.fm.20251001.12

Research Article |

| Peer-Reviewed

Hydromagnetic Boundary Layer Flow and Heat Migration of Dual Stratified Eyring-Powell Fluid

Simon Waswa Wekesa

, Winfred Nduku Mutuku

Published in Fluid Mechanics (Volume 10, Issue 1)

Received: 10 May 2025 Accepted: 28 May 2025 Published: 23 June 2025

Views: Downloads:

Download PDF

Share This Article

Twitter
Linked In
Facebook

Abstract

The Eyring-Powell liquid is a type of non-Newtonian fluid. The complex flow behavior makes it useful in a variety of industrial and engineering applications such as drug manufacturing, paint and in armor construction. Blood, starch, nail polish and honey are such examples. The viscosity of these fluid changes with the rate at which the fluid shears. The need for improved heat transport fluid for industrial processes necessitates this research. The existing fluid are outdated by the advance in technology of machines. This paper modifies the classic Navier-Stokes equations to better capture the unique features of these fluids. The effect of a dual-layer structure on heat transfer in the hydromagnetic flow of an Eyring-Powell fluid near a boundary is numerically investigated. The state variable technique is used to generate and linearize the governing nonlinear differential equations as well as the applicable boundary conditions. The predictor-corrector scheme is utilized to solve the equations by calling the ode113 solver in matlab as the bvp5c function is employed for analysis. The predictor makes the first approximation which is refined by the corrector. The findings, graphically depicted, demonstrate that fluid velocity, temperature, and other parameters decrease with increasing magnetic field intensity, thermal stratification, concentration stratification, and Nusselt number.

Published in	Fluid Mechanics (Volume 10, Issue 1)
DOI	10.11648/j.fm.20251001.12
Page(s)	11-20
Creative Commons	This is an Open Access article, distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution and reproduction in any medium or format, provided the original work is properly cited.
Copyright	Copyright © The Author(s), 2025. Published by Science Publishing Group

Keywords

Hydromagnetic, Boundary Layer, Stratification, Thermophoresis, Fluid

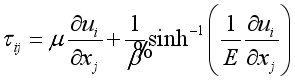1. Introduction

This scholarly work aims to deepen understanding and practical application through rigorous research, focusing on a model derived from the kinetic theory of matter that has enhanced the study of non-Newtonian fluids. The model is defined by three key constants: the Eyring-Powell parameter (ϵ), the material fluid parameter (γ), and the non-Newtonian parameters (ω), which together ensure a nonzero, bounded viscosity at both the surface and at infinity. Non-Newtonian fluid dynamics play a crucial role in industries like petroleum drilling, polymer production, glass manufacturing, and metal processing, while polymers are widely used in agriculture, medicine, and electronics for coating purposes. Additionally, magnetic fields are employed to analyze fluid behaviour, particularly the effects of particle alignment and flux rate under varying conditions, with applications in optical switches, magneto-optical filters, and nonlinear opto-materials. Hameed et al.

[15]

studied unsteady MHD of a non-Newtonian electrically conducting fluid on a porous non-conducting plate and discussed the effect of the presence of material constants of the second-order motion on the velocity field. Ibrahim and Makinde.

[8]

discussed and demonstrated the double stratification on boundary layer flow and heat transfer of the nanofluids over a vertical plate, considering Brownian motion, thermophoresis, thermal stratification, and solutal stratification parameters. Javed et al.

[9]

looked into the boundary layer flow of an Eyring-Powell non-Newtonian fluid over a stretching surface of another similar flow and found that the fluid constituted the Eyring-Powell equation. Waini et al.

[13]

delved into Eyring-Powell fluid flow past a shrinking sheet: effect of magnetohydrodynamic (MHD) and Joule heating. The results revealed magnetic parameter growth rose the temperature. Siddiqui et al.

[14]

analysed Eyring-Powell fluid in helical screw rheometer and found out that an increase in the value of non-Newtonian parameters and pressure gradients escalated the flow of the fluid.

Numerically, Malik et al

[10]

described the Eyring-Powell fluid in a magnetic field on the effect of physical parameters on mixed convective flow over a stretching sheet. Anderson

[3]

justified the boundary layer flow condition of how viscosity and the immediate adjacent boundary affect the neighbouring molecules. Sandeep et al

[5]

presented heat and mass transfer in MHD nanofluid flow due to a cone in the porous medium. Ramzan et al.

[17]

studied radiative flow of Powell-Eyring magneto-nanofluid over a stretching cylinder with chemical reaction and double stratification near a stagnation point. The growth of thermal and solutal stratification deescalated temperature and concentration. Verma et al.

[19]

probed the boundary layer flow of non-Newtonian Eyring–Powell nanofluid over a moving flat plate in Darcy porous medium with a parallel free-stream with multiple solutions and stability analysis. The rate of mass transfer dwindled with rise in Eyring-Powell parameter. Abbas & Megahed

[6]

looked into Powell-Eyring fluid flow over a stratified sheet through porous medium with thermal radiation and viscous dissipation. Results, among other findings presented cooling increased by raising thermal stratification parameter. Jamshed et al.

[7]

probed a numerical frame work of magnetically driven Powell-Eyring nanofluid using single phase model. Temperature improved the function of Biot number.

Faiza et al.

[1]

studied MHD on the bi-convective motion of Eyring-Powell nanofluid over a stretched surface, where they discussed the role of gyrotactic micro-organisms in heat and mass transfer in the presence of MHD forces in Eyring-Powell fluid. Mahanthesh et al.

[16]

investigated the unsteady MHD three-dimensional flows induced by a stretching surface to study the effects of thermal radiation, viscous dissipation, and Joule heating on velocity, temperature, and nanoparticle concentration. Aznidar Ismail et al.

[21]

discussed MHD Boundary Layer Flow in Double Stratification Medium and posted thermal stratification declined temperature.

Mutuku and Makinde

[11]

examined double stratification on mass and heat transfer in unsteady MHD nanofluid flow over a flat surface. The results indicated that thermal stratification reduced fluid temperature while solutal stratification reduced nanoparticle concentration. Srinivasacharya and Surender

[18]

presented the effect of double stratification on mixed convection boundary layer flow of a nanofluid past a vertical plate in a porous medium in which thermophoresis lowered heat transfer rate while it hiked the rate of mass and nanoparticle transport. Ramana Reddy et al.

[12]

looked into the effect of Soret and Dufour numbers on chemically reacting Eyring-Powell fluid flow over an exponentially stretching sheet with thermal radiation and the consequences of heat and mass transfer in the boundary layer flow. Akinshilo et al.

[2]

researched and illustrated the analysis of Eyring-Powell fluid flow with temperature-dependent viscosity and internal heat generation.

Asha and Sunitha

[4]

discussed the effect of Joule Heating and MHD on the peristaltic blood flow of a nanofluid in a non-uniform channel. The results depicted that the pressure gradient gave opposite behaviour with increasing values of Eyring-Powell parameters.

Our model studies steady double stratification on MHD boundary layer flow and heat transfer of Eyring-Powell fluid, since nothing is posted about it.

2. Equations

According to Eyring and Powell (1944), the Cauchy stress tensor in the Eyring-Powell fluid is given by

(1)

where

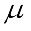is the dynamic viscosity coefficient,

\overset{̌}{β}

and

E

are the Eyring-Powell and rheological fluid parameters,

τ_{i, j}

is the shear stress tensor component and

\sinh^{- 1}

is the inverse hyperbolic sine function. From equation (1), Ali and Zaib (2019) approximated sinh^-1 as

\sinh^{- 1} (\frac{1}{E} \frac{{\partial u}_{i}}{{\partial x}_{j}}) ≅ \frac{1}{E} \frac{{\partial u}_{i}}{{\partial x}_{j}} - \frac{1}{6} {(\frac{1}{E} \frac{{\partial u}_{i}}{{\partial x}_{j}})}^{3}

The fluid flow considered was under low shear stress,

\frac{1}{E} \frac{{\partial u}_{i}}{{\partial x}_{j}} ≪ 1

and

\frac{{\partial u}_{i}}{{\partial x}_{j}}

as the velocity ratio gradient.

τ_{ij} = μ \frac{\partial u_{i}}{\partial x_{j}} + \frac{1}{\tilde{β}} (\frac{1}{E} \frac{{\partial u}_{i}}{{\partial x}_{j}} - \frac{1}{6} {(\frac{1}{E} \frac{{\partial u}_{i}}{{\partial x}_{j}})}^{3})

(2)

The variables governing the flow in this study were chosen as velocity

(u, v)

, temperature,

T

and concentration,

C

Download: Download full-size image

Figure 1. Flow geometry.

By positioning the x-axis horizontally along the direction of the moving fluid and the y-axis perpendicular to it, a uniform magnetic field is applied perpendicular to the surface and parallel to the y-axis. The fluid studied is a non-Newtonian Eyring-Powell fluid with finite electrical conductivity. The parameters of this fluid constrain variations in its properties. According to Jaber

[20]

, due to the fluid's unlimited electrical conductivity, the effects of viscous dissipation, Joule heating, induced magnetic field, external electric field, and flux polarity are negligible in the analysis. Utilizing the boundary layer approximation for the Eyring-Powell fluid and the stated assumptions, Boussinesq’s equation was employed to derive the continuity, momentum, energy, and concentration equations for steady, incompressible flow. The steady, incompressible Eyring-Powell fluid flow equations were formulated as follows:

The steady incompressible Eyring-Powell fluid flow equations were obtained considering the laws of conservation of

Mass:

Div (

\vec{V}

) =0 (3)

Linear momentum:

\vec{V} . grad \vec{V} = - \frac{1}{ρ} grad p + ν \nabla^{2} \vec{V} + \vec{F}

(4)

Energy:

(\vec{V} . grad) T = \frac{μ}{{ρC}_{p}} \nabla^{2} T

(5)

Diffusion:

(\vec{V} . grad) C = D \nabla^{2} C - (div \vec{ν_{T}} C)

(6)

With

\vec{V}

as the velocity vector, p is the pressure, and

ν

is the kinematic coefficient of viscosity,

\vec{F}

is the imposed magnetic force, and g is the acceleration due to gravity. Based on the stated assumptions, the formulation of equations governing boundary layer flow were obtained as

\frac{\partial u}{\partial x} + \frac{\partial v}{\partial y}

= 0 (7)

u \frac{\partial u}{\partial x} + v \frac{\partial u}{\partial y}

(ν + \frac{1}{ρ \overset{̌}{β} C}) \frac{\partial^{2} u}{{\partial y}^{2}} - \frac{1}{2 ρ \overset{̌}{β} C^{3}} {(\frac{\partial u}{\partial y})}^{2} (\frac{\partial^{2} u}{{\partial y}^{2}}) + \frac{1}{ρ_{f}} [(C - C_{\infty}) ρ_{f} β_{o} g (T - T_{\infty}) - (ρ_{p} - ρ_{f}) g (C - C_{\infty})] - \frac{σ B^{2} (t) (u - u_{\infty})}{ρ}

(8)

u \frac{\partial T}{\partial x} + v \frac{\partial T}{\partial y}

\frac{k}{ρ c_{p}} \frac{\partial^{2} T}{{\partial y}^{2}}

\frac{μ}{ρ c_{p}} {(\frac{\partial u}{\partial y})}^{2} + \frac{σ B^{2} (t) {(u - U_{\infty})}^{2}}{ρ c_{p}}

(9)

u \frac{\partial C}{\partial x} + v \frac{\partial C}{\partial y}

D_{B} \frac{\partial^{2} u}{{\partial y}^{2}}

(10)

and the boundary conditions at the surface of the sheet and the free stream were expressed as;

\begin{matrix} u = 0, v = v_{w} (x), T = T_{w} (x), C = C_{w} (x) at y = 0 \\ u \to u_{\infty} (x), T \to T_{\infty} (x), C \to C_{\infty} (x), as y \to \infty \end{matrix}\}

(11)

where u and v are the velocity components along the x-axis and y-axes, respectively,

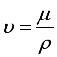the kinematic viscosity,

the thermal conductivity of the fluid,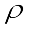

the fluid density,

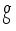the acceleration due to gravity,

the volumetric expansion coefficient of the fluid,

T_{w}

temperature,

C_{w}

the particle volume fraction on the boundary of the magnetic field, D the Brownian motion coefficient,

U_{\infty}

the ambient free stream velocity,

T_{\infty}

ambient temperature,

C_{\infty}

ambient concentration, μ the fluid coefficient of dynamic viscosity and

B_{o}

the imposed magnetic field.

The

λ

t < 1, a, b, c, m, and n are positive constants and

λ

with dimension (time)^-1 is the unsteadiness frequency parameter. Positive values of b, c, m, and n corresponded to the assisting flows while the negative the opposing flows.

In non-dimensionalization, the set of equations describing motion were partial differential equations that, through similarity, were transformed into nonlinear equations and converted into ordinary differential equations. In order to simplify, the following dimensionless variables were introduced.

\begin{matrix} η = {(\frac{a}{νx})}^{\frac{1}{2}} y, ψ = {(av)}^{\frac{1}{2}} xf (η) \\ θ (η) = \frac{T - T_{\infty}}{T_{ω} - T_{\infty}} \\ ϕ (η) = \frac{C - C_{\infty}}{C_{ω} + C_{\infty}} \end{matrix}]

(12)

Where

η and ψ

are the similarity and the stream function variables that were defined as

u = \frac{\partial ψ}{\partial y}

and

v = - \frac{\partial ψ}{\partial x}

(13)

substituting Eqn. (13) into equation (7) satisfied it. By appropriate differentiation and substitution of equation (12) into (8-10), equation (14) was obtained as

\begin{matrix} (1 + ϵ) f^{'''} - γ Ω {(f^{''})}^{2} f^{'''} - {(f^{'})}^{2} + f f^{''} + Grθ + Gr β_{1} - Nr (ϕ - β_{2}) - M (f^{'} - 1) = 0 \\ θ^{''} + PrEc {(f^{''})}^{2} + \Pr f^{'} θ - \Pr f^{'} β_{1} + {Prθ}^{'} f + PrEcM {(f^{'} - 1)}^{2} = 0 \\ ϕ^{''} + Le [f' ϕ + {f' β}_{2} - ϕ' f] = 0 \end{matrix}]

(14)

Subject to the dimensionless boundary conditions

f^{'} = 0, f^{'} = f, θ = 1 - β_{1}, ϕ = 1 - β_{2}, θ = 0, ϕ = 0

(15)

The parameters were prescribed as

ϵ = \frac{1}{μ \overset{̅}{B} C}, Le = \frac{v}{∆_{B}}, M = \frac{σ B_{0}^{2}}{ρa}, \Pr = \frac{k}{μ C_{p}}, Nr = (\frac{T_{w} - T_{\infty}}{ρ_{f} a^{2}}) g

β_{1} = \frac{c}{b}

β_{2} = \frac{n}{m}

γ = \frac{1}{μ \hat{β} C^{3}}, Gr = \frac{(1 - C_{\infty}) gβ}{a^{2}}

Ω = \frac{{a^{3} x}^{2}}{2 v C^{2}}

and

Ec = \frac{a^{2} x}{b C_{p}}

Where

ϵ, Le, M, \Pr, Nr, β_{1}, β_{2}, γ, Gr, Ω, Ec

are the dimensionless Eyring-Powell parameter, Lewis number, Magnetic parameter, Prandtl number, thermophoresis parameter, Thermal stratification parameter, solutal stratification parameter, material fluid parameter, Grashoff number, local non-Newtonian parameter, and Eckert number respectively.

The physical quantities, skin friction coefficient

C_{f},

Nusselt number

Nu

and Sherwood number

Sh

, applied in industries and engineering fields were stated as

C_{f} = \frac{τ_{ω}}{ρ u_{\infty}^{2}}, Nu = \frac{x q_{ω}}{k (T_{ω} - T_{\infty})}, Sh = \frac{x q_{m}}{D_{m} (ρ_{p} - ρ_{f})}

(16)

τ_{ω}

q_{ω}

and

q_{m}

are skin friction, surface heat flux, and the surface mass flux defined by

τ_{ω} = μ \frac{\partial u}{\partial y}, q_{ω} = k \frac{\partial T}{\partial y}

and

q_{m} = {- D}_{m} \frac{\partial C}{\partial y}

(17)

The

μ

k

are dynamic viscosity and thermal conductivity. Applying equation (17) into equation (16), we obtained

{Re}_{x}^{\frac{1}{2}} C_{f} = f^{''} (0), {Re}_{x}^{\frac{- 1}{2}} Nu = - θ^{'} (0), {Re}_{x}^{\frac{1}{2}} Sh = - ϕ' (0)

(18)

The quantities

C_{f}

, Nu, Sh were the local skin friction, Nusselt number, and Sherwood number,

{Re}_{x} = U_{\infty} x / ν

was the local Reynolds number.

3. Numerical Procedure

The boundary value problem solver bvp5c was called by invoking the Matlab ode113 function that solved the linearized equations.

f = y_{1}, f^{'} = y_{2}, f^{''} = y_{3}, f^{'''} = y_{4}, θ = y_{4}, θ^{'} = y_{5}, θ^{''} = y_{6}, ϕ = y_{6}, ϕ^{'} = y_{7}

y_{1}^{'} = y_{2}

(19)

y_{2}^{'} = y_{3}

(20)

y_{3}^{'} = \frac{y_{2}^{2} - y_{1} y_{3} - Gr y_{4} - Gr β_{1} + Nr (y_{6} - β_{2}) + M (y_{2} - 1)}{(1 + ϵ - γω y_{3}^{2})}

(21)

{y_{5}^{'} = y}_{5}

(22)

y_{5}^{'} = \Pr y_{2} β_{1} - PrEc y_{3}^{2} - \Pr y_{2} y_{4} - \Pr y_{5} y_{1} - PrEcM {(y_{2} - 1)}^{2}

(23)

y_{6}^{'} = y_{7}

(24)

y_{7}^{'} = - Le [y_{2} y_{6} + {y_{2} β}_{2} - y_{7} y_{1}]

(25)

constrained by the boundary conditions

\begin{matrix} y_{2} = f_{ω}, y_{4} = 1 - β_{1}, y_{7} = 1 - β_{2} at η = 0 \\ y_{2} = 1, y_{5} = 0, y_{6} = 0 at η = \infty \end{matrix}\}

(26)

4. Discussion

The nonlinear momentum, temperature, and concentration equations Eqn. (13) with the boundary conditions Eqn. (14) were transformed to linear differential equations. Execution of the Adams-Moulton predictor-corrector in Matlab ode113, demystified numerical computation. 1000 mesh densities were used with absolute and relative tolerance of 10^-6and 10^-8. The characteristic length

0 \leq η \leq 8

and the convergence criterion was deployed during simulation. The effects of the varied magnetic field, thermophoresis, thermal stratification, and solutal stratification parameters on dimensionless velocity, dimensionless temperature, dimensionless concentration, local skin friction, local Nusselt number, and local Sherwood number were discussed.

Velocity profiles

Download: Download full-size image

Figure 2. Effect of M on dimensionless velocity.

β_{1} = 0.1, β_{2} = 0.5, \in = 0.4, Ec = 0.3, \Pr = 0.4, Gr = 0.3,

G = 0.1, Le = 0.3, γ = 0.2; Ω = 0.3, Nr = 0.25

As observed in figure 3, an increase in the thermophoresis parameter leads to a decrease in the velocity of the fluid. The increase of particles in the fluid medium at constant temperature and volume leaves little space for migration. Also, the force driving these particles lowers.

Download: Download full-size image

Figure 3. Effect of Nr on dimensionless velocity.

β_{1} = 0.1, β_{2} = 0.5, \in = 0.4, Ec = 0.3, \Pr = 0.4, Gr = 0.3,

G = 0.1, Le = 0.3, γ = 0.2, Ω = 0.3

Download: Download full-size image

Figure 4. Effect of

β_{1}

on dimensionless velocity.

β_{2} = 0.1, E = 0.2, Ec = 0.3, \Pr = 0.7, Gr = 0.2, G = 0.1,

Le = 0.03, γ = 0.5, Ω = 0.4, Nr = 0.1

Figures 2-5 show the effects of magnetic field, thermophoretic, thermal, and solutal stratification parameters on fluid velocity.

Figure 2 confirms

[21]

the effect of strength of magnetic field increasing decreases velocity. The application of magnetic field strength perpendicularly introduces a resistance force, Lorentz force, which reduces the rate at which the fluid particles move hence reducing the flow rate thus satisfying the first boundary condition.

Download: Download full-size image

Figure 5. Effect of

β_{2}

on dimensionless velocity.

β_{1} = 0.8, \in = 0.2, Ec = 0.3, \Pr = 0.7, Gr = 0.2, G = 0.1,

Le = 0.03, M = 0.1, γ = 0.5, Ω = 0.4; Nr = 0.1

From figure 4, a growth of thermal stratification diminishes the velocity of the fluid. The fluid layers order according to temperature decay and the thermal floating (thermal buoyancy). The rate at which energy flows from one stratum to another reduces as velocity.

Figure 5 depicts that a rise in solutal stratification depletes velocity. An increased particle concentration decreases the magnitude of vibration and the movement of the fluid particles causing a reduction in the flow rate.

Temperature profiles

Download: Download full-size image

Figure 6. Effect of M on dimensionless temperature.

β_{1} = 0.8, β_{2} = 0.1, \in = 0.2, Ec = 0.3, \Pr = 0.7, Gr = 0.2,

G = 0.1, Le = 0.03, γ = 0.5, Ω = 0.4, Nr = 0.1

It is observed that, Figure 6, magnetic field increases with temperature of the fluid. The Lorentz force causes resistance against particles in the fluid medium. The motion of the particles in the resistive medium cause heat climbing temperature.

Download: Download full-size image

Figure 7. Effect of

β_{1}

on dimensionless temperature.

β_{2} = 0.1, \in = 0.2, Ec = 0.3, \Pr = 0.7, Gr = 0.2, G = 0.1,

Le = 0.03, M = 0.1, γ = 0.5, Ω = 0.4, Nr = 0.1

Download: Download full-size image

Figure 8. Effect of

β_{2}

on dimensionless temperature.

β_{1} = 0.4, \in = 0.2, Ec = 0.3, \Pr = 0.7, Gr = 0.2, G = 0.1,

Le = 0.03, M = 0.1, γ = 0.5, Ω = 0.4, Nr = 0.1

Download: Download full-size image

Figure 9. Effect of Nr on dimensionless temperature.

β_{1} = 0.4, β_{2} = 0.1, \in = 0.2, Ec = 0.3, \Pr = 0.7, Gr = 0.2, Gr = 0.1,

Le = 0.03, M = 0.1, γ = 0.5

In Figure 7, it is clear that thermal stratification decreases temperature. Layering a fluid according to temperature exchanges heat between the neighboring particles in adjacent layers. This exchange occurs until the particles on the boundaries equilibrate. Some fluid particles lose energy while others gain. The loss-gain lowers the temperature.

As illustrated in Figure 8, solutal stratification cutbacks ambient and fluid temperature. Momentum transport heat from warmer to cold regions. Layering resists vertical flow of heat. The upper stratum lose heat faster to the surroundings thus it is replenished from below. Solutal gradients barricades thermal mixing creating unequal temperature caused by radiation and conduction. Heat transfer to ambient domains cutdown.

Figure 9 shows a declining temperature heighten thermophoresis parameter. Low-temperature gradient and Brownian motion due to the collision of particles lowers the temperature. Temperature difference between hot and cold regions moves suspended particles to the cold regions. The collision yield momentum force and higher kinetic energy.

Concentration profiles

Download: Download full-size image

Figure 10. Effect of M on dimensionless concentration.

β_{1} = 0.4, β_{2} = 0.1, \in = 0.2, Ec = 0.3, \Pr = 0.7, Gr = 0.2, G = 0.1,

Le = 0.03, M = 0.8, γ = 0.1, Ω = 0.4, Nr = 0.8

Download: Download full-size image

Figure 11. Effect of

β_{1}

on dimensionless concentration.

β_{2} = 0.1, \in = 0.2, Ec = 0.3, \Pr = 0.7, Gr = 0.5, G = 0.1, Le = 0.03,

M = 0.1, γ = 0.1, Ω = 0.3, Nr = 0.4

Download: Download full-size image

Figure 12. Effect of

β_{2}

on dimensionless concentration.

β_{1} = 0.1, \in = 0.2, Ec = 0.3, \Pr = 0.7, Gr = 0.5, G = 0.1, L = 0.03,

M = 0.1, γ = 0.1, Ω = 0.3, Nr = 0.4

Download: Download full-size image

Figure 13. Effect of Nr on dimensionless concentration.

β_{1} = 0.1, β_{2} = 0.2, \in = 0.3, Ec = 0.4, \Pr = 0.7, Gr = 0.5,

G = 0.1, Le = 0.3, M = 0.4, γ = 0.3, Ω = 0.3

Figure 10 shows that magnetic field strength advances with particle concentration. Particles are charged and squeezed together. Thermal stratification increases concentration (Figure 11) because particles with the same temperature are layered together. Particle concentration is highest on the boundary since temperature and diffusion forces are low, while it underdevelopes with a hike in solutal stratification (Figure 12); size and density arrange the particles.

Thermophoresis sores the concentration of the fluid particles (Figure 13). The energy gradient accummulates particles to cooler regions. Thi is applied in the concentration of deoxyrebonulceic acid in biofilms and the sceintific justification of why particles deposit on cooler surfaces.

The Particles possessing more energy flow to the cold region while those with lower energy move towards the higher temperature. The resultant effect is that thermophoretic particles lose some fluid into the air as vapor. The fluid saturates.

Download: Download full-size image

Figure 14. Effects of M and

γ

on dimensionless concentration.

β_{1} = 0.1, β_{2} = 0.6, \in = 1, Ec = 0.6, \Pr = 1.2, Gr = 3,

G = 2, Le = 0.9, γ = 1, Ω = 0.3, Nr = 0.3

Download: Download full-size image

Figure 15. Effects of M and

γ

on Local Nusselt Number.

β_{1} = 0.01, β_{2} = 0.2, \in = 0.2, Ec = 1.2, \Pr = 4, Gr = 1.5,

G = 0.4, Le = 0.8, γ = 0.1, Ω = 0.6, Nr = 0.4

Download: Download full-size image

Figure 16. Effects of

β_{1} and Nr

on Local Nusselt Number.

β_{2} = 0.3, \in = 0.4, Ec = 1.3, \Pr = 4, Gr = 1.2, G = 0.6,

Le = 0.95, M = 0.4, γ = 0.1, Ω = 0.6

Download: Download full-size image

Figure 17. Effects of M

and Nr

of Local Sherwood Number.

β_{1} = 0.1, β_{2} = 0.8, \in = 1.2, Ec = 0.4, \Pr = 6, Gr = 0.8,

G = 1.1, Le = 1.2, γ = 0.4, Ω = 0.1

Download: Download full-size image

Figure 18. Effects of

β_{1} and Nr

of Local Sherwood Number.

β_{2} = 0.01, β_{2} = 0.8, \in = 1.1, Ec = 0.4, \Pr = 8, Gr = 0.8,

G = 1.1, Le = 1.2, M = 0.1, γ = 0.4; Ω = 0.1

Download: Download full-size image

Figure 19. Effects of

β_{2} and Nr

of Local Sherwood Number.

β_{1} = 0.01, \in = 0.9, Ec = 0.4, \Pr = 4, Gr = 0.8, G = 1.2,

Le = 1.5, M = 0.1, γ = 0.4, Ω = 0.1

Effect of variation of parameters on

C_{f}, Sh and Nu

Figures 14 to 19 illustrates the effect of differently varied fluid parameters on Eyring-Powell fluid for local skin friction, Nusselt number, and Sherwood number. The variants are fluid parameters, magnetic fields strength, thermal stratification, and solutal stratification. An inflation of magnetic field strength and fluid parameter shrinks the local skin friction (Figure 14) because both parameters shift the fluid away from the boundaries. Figure 15 indicates that energy transfer improves with magnetic field strength and thermal diffusion. An increase in thermal stratification and thermophoresis parameter trims energy diffusion as observed on Figures 16 and 17 respectively. Figure 19 shows that mass migration flourishes with thermophoresis parameter and magnetic field strength. The spread of particles due to Brownian motion spreads mixing. Figure 19 Illustrates the augmentation of solutal stratification and thermophoresis parameters declines mass diffusion.

5. Conclusion

A synopsis of the numerical analysis of double stratification on magnetohydrodynamic boundary layer flow and heat transfer of an Eyring-Powell fluid is presented. The nonlinear governing partial differential equations obtained have been linearized using similarity transformations. The numerical results are illustrated graphically for velocity, temperature and concentration, skin friction coefficient, local Nusselt number, and the local Sherwood number. The study reveals the following:

1) The development of magnetic field strength, thermophoresis, thermal stratification, and solutal stratification decays velocity.

2) A climb of thermal stratification, solutal stratification, and thermophoresis parameters lowers the temperature.

3) The fluid concentration grows with magnetic field strength, thermal stratification, solutal stratification, and thermophoresis.

4) An increase in magnetic field and material fluid

decreases skin friction, while an increase in magnetic strength, thermal stratification and thermophoresis increases energy and mass.

5) The rise of thermal stratification, solutal stratification and thermophoresis diminishes energy and mass diffusion.

There is a possibility of further study with the inclusion of the z-axis for three-dimensional analysis. Finally, one can consider the time variable for unsteadiness flow analysis.

Greek Letters and Symbols

$γ$	Material Parameter
$ω$	Non-Newtonian Parameter
$ϵ$	Eyring-Powell Parameter
$μ$	Dynamic Viscosity
$B_{o}$	Initial Magnetic Field
$λ$	Unsteadiness Parameter
$ψ$	Dimensionless stream function
$ϕ$	Dimensionless Concentration function
$θ$	Dimesnionless Temperature function
$τ_{ω}$	Skin Friction
$β_{1}$	Thermal Stratification
$β_{2}$	Solutal Stratification
$ρ$	Density
Ω	Local Nanomaterial Parameter
$η$	Similarity Variable
$\nabla$	Nabla Operator
$\vec{V}$	Velocity Vector
Ec	Eckert Number
Gr	Grashof Number
Nr	Thermophoresis
M	Magnetic field
g	Gravitational Field Strength
T	Temperature
Le	Lewis Number
F	Force
p	Pressure
Pr	Prandtl Number
Nu	Nuselt Number
Sh	Sherwood Number
$C_{f}$	Local Skin friction
$C_{p}$	Specific heat capacity
${Re}_{x}$	Reynold number
$q_{ω}$	surface heat flux
$q_{m}$	surface mass flux
k	thermal conductivity
a,b,c	Constants
t	time
$T_{\infty}, C_{\infty}, u_{\infty}$	Ambient Temperature, Concentration & Velocity
(u,v)	Speed in x and y Directions

Abbreviations

MHD	Magnetohydrodynamic
Matlab	Matrix Laboratory
Eqn.	Equation

Acknowledgments

I express by gratitude to Kenyatta University for providing the resources and the support. Thanks to the teaching fraternity in the Department of Mathematics and Actuarial Sciences particularly, my supervisor Professor Mutuku Winny for her vast knowledge, experience in fluid mechanics and insightful guidance and encouragement. My appreciation goes to the departmental secretariate and the University administration. Finally, my sincere gratitude to the reviewers of this article for their comprehensive, proper review and recommendations.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Ali, F and Zaib, A. Unsteady flow of an Eyring-Powell nanofluid near stagnation point past a convectively heated stretching sheet, Arab Journal of Basic and Applied Science, 2019, VOL. 26, NO. 1, 215–224, https://doi.org/10.1080/25765299.2019.1603586
[2]	Akinshilo, A. T. and Olaye, O. (2019) 'On the analysis of the Eyring Powell model-based fluid flow in a pipe with temperature-dependent viscosity and internal heat generation, Journal of King Saud University - Engineering Sciences. King Saud University, 31(3), pp. 271–279. https://doi.org/10.1016/j.jksues.2017.09.001
[3]	Anderson, J. D. (2005) 'Ludwig Prandtl's boundary layer, Physics Today, 58(12), pp. 42–48. https://doi.org/10.1063/1.2169443
[4]	Asha, S. K., and Sunitha, G. (2019) 'Effect of Joule heating and MHD on peristaltic blood flow of Eyring–Powell nanofluid in a non-uniform channel', Journal of Taibah University for Science. Taylor & Francis, 13(1), pp. 155–168. https://doi.org/10.1080/16583655.2018.1549530
[5]	Babu, M. J., Sandeep, N. and Raju, C. S. K. (2016) 'Heat and mass transfer in MHD Eyring-Powell nanofluid flow due to cone in the porous medium, International Journal of Engineering Research in Africa, 19, pp. 57–74. https://doi.org/10.4028/www.scientific.net/JERA.19.57
[6]	Abbas, W., & Megahed, A. M. (2021). Powell-eyring fluid flow over a stratified sheet through porous medium with thermal radiation and viscous dissipation. AIMS Mathematics, 6(12), 13464–13479. https://doi.org/10.3934/math.2021780
[7]	Jamshed, W., Eid, M. R., Nisar, K. S., Nasir, N. A. A. M., Edacherian, A., Saleel, C. A., & Vijayakumar, V. (2021). A numerical frame work of magnetically driven Powell-Eyring nanofluid using single phase model. Scientific Reports, 11(1), 1–26. https://doi.org/10.1038/s41598-021-96040-0
[8]	Ibrahim, W. and Makinde, O. D. (2013) 'The effect of double stratification on boundary-layer flow and heat transfer of nanofluid over a vertical plate', Computers and Fluids. Elsevier Ltd, 86, pp. 433–441. https://doi.org/10.1016/j.compfluid.2013.07.029
[9]	Javed, T. et al. (2013) 'Flow of an Eyring-Powell non-newtonian fluid over a stretching sheet, Chemical Engineering Communications, 200(3), pp. 327–336. https://doi.org/10.1080/00986445.2012.703151
[10]	Malik, M. Y. et al. (2015) 'Mixed convection flow of MHD Eyring-Powell nanofluid over a stretching sheet: A numerical study, Dalton Transactions, 5(11). https://doi.org/10.1063/1.4935639
[11]	Mutuku, W. N. and Makinde, O. D. (2017) 'Double stratification effects on heat and mass transfer in unsteady MHD nanofluid flow over a flat surface', Asia Pacific Journal on Computational Engineering. Springer Singapore, 4(1). https://doi.org/10.1186/s40540-017-0021-2
[12]	Ramana Reddy, J. V., Sugunamma, V. and Sandeep, N. (2018) 'Impact of short and Dufour numbers on MHD Casson fluid flow past an exponentially stretching sheet with non-uniform heat source/sink', Defect and Diffusion Forum, 388(4), pp. 14–27. https://doi.org/10.4028/www.scientific.net/DDF.388.14
[13]	Waini, I., Ishak, A., & Pop, I. (2024). Eyring-Powell Fluid Flow Past a Shrinking Sheet: Effect of Magnetohydrodynamic (MHD) and Joule Heating. Journal of Advanced Research in Fluid Mechanics and Thermal Sciences, 116(1), 64–77. https://doi.org/10.37934/arfmts.116.1.6477
[14]	Siddiqui, A. M., Haroon, T., & Zeb, M. (2014). Analysis of eyring-powell fluid in helical screw rheometer. The Scientific World Journal, 2014. https://doi.org/10.1155/2014/143968
[15]	Hameed, M. and Nadeem, S. (2007) 'Unsteady MHD flow of non-Newtonian fluid on a porous plate', Journal of Mathematical Analysis and Applications, 325(1), pp. 724–733. https://doi.org/10.1016/j.jmaa.2006.02.002
[16]	Mahanthesh, B., Gireesha, B. J. and Gorla, R. S. R. (2017) 'Unsteady three-dimensional MHD flow of a nano Eyring-Powell fluid past a convectively heated stretching sheet in the presence of thermal radiation, viscous dissipation, and Joule heating, Journal of the Association of Arab Universities for Basic and Applied Sciences. University of Bahrain, 23, pp. 75–84. https://doi.org/10.1016/j.jaubas.2016.05.004
[17]	Ramzan, M., Bilal, M., & Chung, J. D. (2017). Radiative flow of powell-eyring magneto-nanofluid over a stretching cylinder with chemical reaction and double stratification near a stagnation point. PLoS ONE, 12(1), 1–19. https://doi.org/10.1371/journal.pone.0170790
[18]	Srinivasacharya, D. and Surender, O. (2015) 'Effect of double stratification on mixed convection boundary layer flow of a nanofluid past a vertical plate in a porous medium', Applied Nanoscience (Switzerland), 5(1), pp. 29–38. https://doi.org/10.1007/s13204-013-0289-7
[19]	Verma, A. K., Gautam, A. K., Bhattacharyya, K., Banerjee, A., & Chamkha, A. J. (2021). Boundary layer flow of non-Newtonian Eyring–Powell nanofluid over a moving flat plate in Darcy porous medium with a parallel free-stream: Multiple solutions and stability analysis. Pramana - Journal of Physics, 95(4). https://doi.org/10.1007/s12043-021-02215-9
[20]	Jaber, K. K. (2014). Effects of Viscous Dissipation and Joule Heating on Mhd Flow of a Fluid With Variable Properties Past A stretching Vertical Plate. 10(33), 383–393.
[21]	Aznidar Ismail, N. S., Abd Aziz, A. S., Ilias, M. R., & Soid, S. K. (2021). MHD boundary layer flow in double stratification medium. Journal of Physics: Conference Series, 1770(1). https://doi.org/10.1088/1742-6596/1770/1/012045

Cite This Article

Plain Text BibTeX RIS

APA Style

Wekesa, S. W., Mutuku, W. N. (2025). Hydromagnetic Boundary Layer Flow and Heat Migration of Dual Stratified Eyring-Powell Fluid. Fluid Mechanics, 10(1), 11-20. https://doi.org/10.11648/j.fm.20251001.12

Copy | Download

ACS Style

Wekesa, S. W.; Mutuku, W. N. Hydromagnetic Boundary Layer Flow and Heat Migration of Dual Stratified Eyring-Powell Fluid. Fluid Mech. 2025, 10(1), 11-20. doi: 10.11648/j.fm.20251001.12

Copy | Download

AMA Style

Wekesa SW, Mutuku WN. Hydromagnetic Boundary Layer Flow and Heat Migration of Dual Stratified Eyring-Powell Fluid. Fluid Mech. 2025;10(1):11-20. doi: 10.11648/j.fm.20251001.12

Copy | Download

@article{10.11648/j.fm.20251001.12,
  author = {Simon Waswa Wekesa and Winfred Nduku Mutuku},
  title = {Hydromagnetic Boundary Layer Flow and Heat Migration of Dual Stratified Eyring-Powell Fluid
},
  journal = {Fluid Mechanics},
  volume = {10},
  number = {1},
  pages = {11-20},
  doi = {10.11648/j.fm.20251001.12},
  url = {https://doi.org/10.11648/j.fm.20251001.12},
  eprint = {https://article.sciencepublishinggroup.com/pdf/10.11648.j.fm.20251001.12},
  abstract = {The Eyring-Powell liquid is a type of non-Newtonian fluid. The complex flow behavior makes it useful in a variety of industrial and engineering applications such as drug manufacturing, paint and in armor construction. Blood, starch, nail polish and honey are such examples. The viscosity of these fluid changes with the rate at which the fluid shears. The need for improved heat transport fluid for industrial processes necessitates this research. The existing fluid are outdated by the advance in technology of machines. This paper modifies the classic Navier-Stokes equations to better capture the unique features of these fluids. The effect of a dual-layer structure on heat transfer in the hydromagnetic flow of an Eyring-Powell fluid near a boundary is numerically investigated. The state variable technique is used to generate and linearize the governing nonlinear differential equations as well as the applicable boundary conditions. The predictor-corrector scheme is utilized to solve the equations by calling the ode113 solver in matlab as the bvp5c function is employed for analysis. The predictor makes the first approximation which is refined by the corrector. The findings, graphically depicted, demonstrate that fluid velocity, temperature, and other parameters decrease with increasing magnetic field intensity, thermal stratification, concentration stratification, and Nusselt number.
},
 year = {2025}
}

Copy | Download

TY - JOUR
T1 - Hydromagnetic Boundary Layer Flow and Heat Migration of Dual Stratified Eyring-Powell Fluid

AU - Simon Waswa Wekesa
AU - Winfred Nduku Mutuku
Y1 - 2025/06/23
PY - 2025
N1 - https://doi.org/10.11648/j.fm.20251001.12
DO - 10.11648/j.fm.20251001.12
T2 - Fluid Mechanics
JF - Fluid Mechanics
JO - Fluid Mechanics
SP - 11
EP - 20
PB - Science Publishing Group
SN - 2575-1816
UR - https://doi.org/10.11648/j.fm.20251001.12
AB - The Eyring-Powell liquid is a type of non-Newtonian fluid. The complex flow behavior makes it useful in a variety of industrial and engineering applications such as drug manufacturing, paint and in armor construction. Blood, starch, nail polish and honey are such examples. The viscosity of these fluid changes with the rate at which the fluid shears. The need for improved heat transport fluid for industrial processes necessitates this research. The existing fluid are outdated by the advance in technology of machines. This paper modifies the classic Navier-Stokes equations to better capture the unique features of these fluids. The effect of a dual-layer structure on heat transfer in the hydromagnetic flow of an Eyring-Powell fluid near a boundary is numerically investigated. The state variable technique is used to generate and linearize the governing nonlinear differential equations as well as the applicable boundary conditions. The predictor-corrector scheme is utilized to solve the equations by calling the ode113 solver in matlab as the bvp5c function is employed for analysis. The predictor makes the first approximation which is refined by the corrector. The findings, graphically depicted, demonstrate that fluid velocity, temperature, and other parameters decrease with increasing magnetic field intensity, thermal stratification, concentration stratification, and Nusselt number.

VL - 10
IS - 1
ER -

Copy | Download

Author Information

Simon Waswa Wekesa

Department of Mathematics and Actuarial Science, Kenyatta University, Nairobi, Kenya

Contact Email

http://orcid.org/0009-0009-4286-9568
Winfred Nduku Mutuku

Department of Mathematics & Actuarial Science, Kenyatta University, Nairobi, Kenya

Contact Email

http://orcid.org/0000-0002-9611-6088

Download PDF

Plain Text BibTeX RIS

APA Style

Wekesa, S. W., Mutuku, W. N. (2025). Hydromagnetic Boundary Layer Flow and Heat Migration of Dual Stratified Eyring-Powell Fluid. Fluid Mechanics, 10(1), 11-20. https://doi.org/10.11648/j.fm.20251001.12

Copy | Download

ACS Style

Wekesa, S. W.; Mutuku, W. N. Hydromagnetic Boundary Layer Flow and Heat Migration of Dual Stratified Eyring-Powell Fluid. Fluid Mech. 2025, 10(1), 11-20. doi: 10.11648/j.fm.20251001.12

Copy | Download

AMA Style

Wekesa SW, Mutuku WN. Hydromagnetic Boundary Layer Flow and Heat Migration of Dual Stratified Eyring-Powell Fluid. Fluid Mech. 2025;10(1):11-20. doi: 10.11648/j.fm.20251001.12

Copy | Download

@article{10.11648/j.fm.20251001.12,
  author = {Simon Waswa Wekesa and Winfred Nduku Mutuku},
  title = {Hydromagnetic Boundary Layer Flow and Heat Migration of Dual Stratified Eyring-Powell Fluid
},
  journal = {Fluid Mechanics},
  volume = {10},
  number = {1},
  pages = {11-20},
  doi = {10.11648/j.fm.20251001.12},
  url = {https://doi.org/10.11648/j.fm.20251001.12},
  eprint = {https://article.sciencepublishinggroup.com/pdf/10.11648.j.fm.20251001.12},
  abstract = {The Eyring-Powell liquid is a type of non-Newtonian fluid. The complex flow behavior makes it useful in a variety of industrial and engineering applications such as drug manufacturing, paint and in armor construction. Blood, starch, nail polish and honey are such examples. The viscosity of these fluid changes with the rate at which the fluid shears. The need for improved heat transport fluid for industrial processes necessitates this research. The existing fluid are outdated by the advance in technology of machines. This paper modifies the classic Navier-Stokes equations to better capture the unique features of these fluids. The effect of a dual-layer structure on heat transfer in the hydromagnetic flow of an Eyring-Powell fluid near a boundary is numerically investigated. The state variable technique is used to generate and linearize the governing nonlinear differential equations as well as the applicable boundary conditions. The predictor-corrector scheme is utilized to solve the equations by calling the ode113 solver in matlab as the bvp5c function is employed for analysis. The predictor makes the first approximation which is refined by the corrector. The findings, graphically depicted, demonstrate that fluid velocity, temperature, and other parameters decrease with increasing magnetic field intensity, thermal stratification, concentration stratification, and Nusselt number.
},
 year = {2025}
}

Copy | Download

TY - JOUR
T1 - Hydromagnetic Boundary Layer Flow and Heat Migration of Dual Stratified Eyring-Powell Fluid

VL - 10
IS - 1
ER -

Copy | Download