In the literature, there are several theoretical and experimental methods for calculating the resonance energies and natural widths of atomic systems. For the 1s22s2p6np ¹P1 series of Ne, Na+, Mg2+, and the 1s2s22p5np ¹P1 series of Ne+, various methods have been employed. In this present work, resonance energies resonance energies and width of the 1s22s2p6 np 1P1 series of the Ne, Na+, Mg2+, and 1s2s22p5 np 1P1 of Ne+ ions are calculated. The energies are calculated in the framework of the Modified Atomic Orbital Theory (MAOT). The results obtained compared very well with theoretical and experimental literature values. The possibility to use the MOAT formalism report rapidly with an excellent accuracy the position of the resonances as well as their width within simple analytical formulae is demonstrated. It is demonstrated that the MOAT-method can be used to assist fruitfully experiments for identifying narrow resonance energies. Thus, our results can be used as reference data for the interpretation of atomic spectra for the diagnosis of astrophysical and laboratory plasma. Through this method new values of these energies are reported going up to n=40. These excellent agreements between theory and experiments indicate that the MAOT formalism can be used to report accurate high-lying excited Rydberg series of atomic species for the diagnostic and the modeling of astrophysical or laboratory plasmas.
| Published in | Nuclear Science (Volume 10, Issue 1) |
| DOI | 10.11648/j.ns.20251001.11 |
| Page(s) | 1-14 |
| Creative Commons |
This is an Open Access article, distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution and reproduction in any medium or format, provided the original work is properly cited. |
| Copyright |
Copyright © The Author(s), 2025. Published by Science Publishing Group |
Photoionization, Resonance Energies, Width, Modified Atomic Orbital Theory, Rydberg Series, Synchrotron Radiation
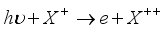
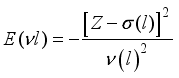 (1)
(1) 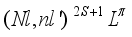 . For the previous term, N denotes the quantum number of the inner electron and n that of the outer electron, their respective orbital quantum numbers are l and l', the total spin is represented by S, L is the total angular momentum, and the parity of the system is represented by π. For the
. For the previous term, N denotes the quantum number of the inner electron and n that of the outer electron, their respective orbital quantum numbers are l and l', the total spin is represented by S, L is the total angular momentum, and the parity of the system is represented by π. For the 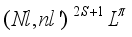 doubly excited states, the total energy of an atomic system of many M electrons is expressed as follows
doubly excited states, the total energy of an atomic system of many M electrons is expressed as follows 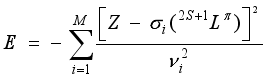 (2)
(2) 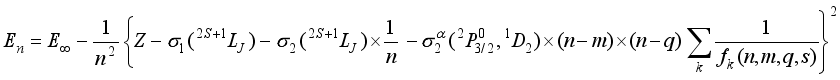 (3)
(3)  screening constants, s denotes the spin of the nl- electron (s = 1/2), E<i><sub></sub></i> is the energy value of the series limit, typically obtained from the NIST atomic database, and Z represents the nuclear charge of the element in question. The only challenge encountered when using the MAOT formalism is related to the determination of the
screening constants, s denotes the spin of the nl- electron (s = 1/2), E<i><sub></sub></i> is the energy value of the series limit, typically obtained from the NIST atomic database, and Z represents the nuclear charge of the element in question. The only challenge encountered when using the MAOT formalism is related to the determination of the 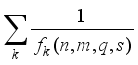 term
term 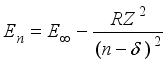 (4)
(4) 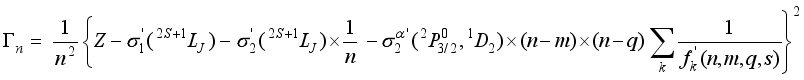 (5)
(5) 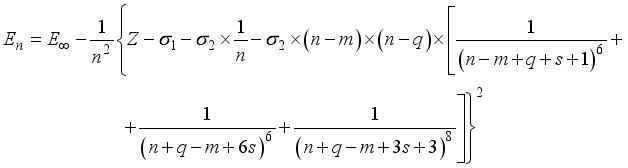 (6)
(6) 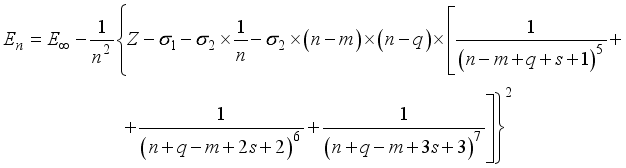 (7)
(7) 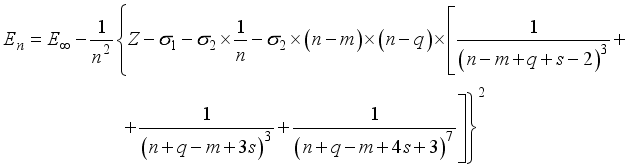 (8)
(8) 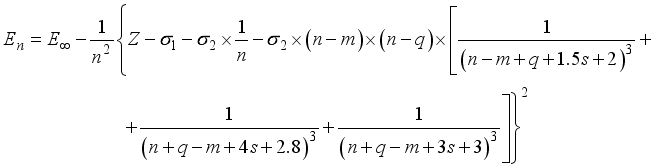 (9)
(9) 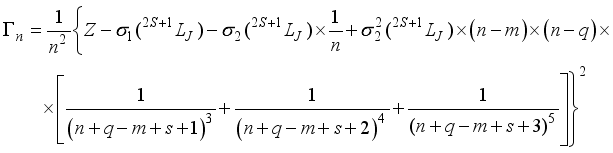 (10)
(10) 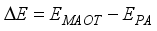 or
or 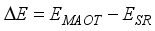 between these levels values at 0,016 eV and 0,014 eV respectively. New theoretical values were found, ranging from n=40. In general, experiments and theories are in perfect agreement.
between these levels values at 0,016 eV and 0,014 eV respectively. New theoretical values were found, ranging from n=40. In general, experiments and theories are in perfect agreement. 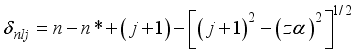 , with z being the asymptotic charge seen by the photoelectron and α the fine-structure constant
, with z being the asymptotic charge seen by the photoelectron and α the fine-structure constant 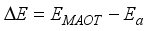 to n = 3 between these levels values at 0,03 eV. After comparison, we can state that our MAOT method allowed us to obtain accurate values up to n = 20. These values are in good agreement with those obtained from Muller's synchrotron radiation
to n = 3 between these levels values at 0,03 eV. After comparison, we can state that our MAOT method allowed us to obtain accurate values up to n = 20. These values are in good agreement with those obtained from Muller's synchrotron radiation States | Theory | Experiment | ||||
|---|---|---|---|---|---|---|
MAOT | SCUNC | NC | SR | PA |
| |
3 | 48.9066 | 48.9066 | 48.9063 | 48.9066 | 48.907 | 0.00 |
4 | 50.5600 | 50.5664 | 50.6496 | 50.56 | 50.565 | 0.00 |
5 | 51.2096 | 51.2494 | 51.3049 | 51.262 | 51.276 | 0.05 |
6 | 51.5260 | 51.5632 | 51.5865 | 51.561 | 51.563 | 0.03 |
7 | 51.7025 | 51.7326 | 51.745 | 51.732 | 51.736 | 0.03 |
8 | 51.8105 | 51.8343 | 51.8419 | 51.8332 | 51.842 | 0.02 |
9 | 51.8811 | 51.9001 | 51.9047 | 51.8975 | 51.898 | 0.02 |
10 | 51.9298 | 51.9452 | 51.9479 | - | - | |
11 | 51.9648 | 51.9773 | 51.9789 | 51.9792 | 0.01 | |
12 | 51.9907 | 52.0011 | 52.0017 | 52.0032 | 0.01 | |
13 | 52.0104 | 52.0192 | 52.0186 | 52.0208 | 0.01 | |
14 | 52.0258 | 52.0332 | 52.0299 | 52.0348 | 0.01 | |
15 | 52.0379 | 52.0444 | 52.0452 | 0.01 | ||
16 | 52.0478 | 52.0534 | 52.0542 | 0.01 | ||
17 | 52.0558 | 52.0607 | ||||
18 | 52.0625 | 52.0668 | ||||
19 | 52.0681 | 52.0719 | ||||
20 | 52.0728 | 52.0762 | ||||
21 | 520768 | 52.0799 | ||||
22 | 52.0803 | 52.0831 | ||||
23 | 52.0833 | 52.0858 | ||||
24 | 52.0859 | 52.0882 | ||||
25 | 52.0882 | 52.0903 | ||||
26 | 52.0903 | 52.0922 | ||||
27 | 52.0921 | 52.0938 | ||||
28 | 52.0937 | 52.0953 | ||||
29 | 52.0951 | 52.0966 | ||||
30 | 52.0964 | 52.0978 | ||||
31 | 52.0975 | |||||
32 | 52.0986 | |||||
33 | 52.0995 | |||||
34 | 52.1004 | |||||
35 | 52.1012 | |||||
36 | 52.1019 | |||||
37 | 52.1026 | |||||
38 | 52.1032 | |||||
39 | 52.1038 | |||||
40 | 52.1043 | |||||
… | ||||||
∞ | 52.114 | 52.114 | ||||
States | Theory | Experiment | ||
|---|---|---|---|---|
MAOT | SCUNC | NC | SR | |
3 | 2.060 | 2.060 | 2.060 | 2.0597 (5) |
4 | 2.959 | 2.965 | 3.049 | 2.963 (7) |
5 | 3.879 | 3.967 | 4.102 | 3.997(12) |
6 | 4.810 | 4.970 | 5.082 | 4.961(13) |
7 | 5.750 | 5.972 | 6.078 | 5.970 (23) |
8 | 6.695 | 6.974 | 7.080 | 6.964 (19) |
9 | 7.644 | 7.976 | 8.075 | 7.933 (28) |
10 | 8.595 | 8.977 | 9.069 | - |
11 | 9.548 | 9.978 | 10.039 | 10.058 (93) |
12 | 10.503 | 10.979 | 11.039 | 11.10 (13) |
13 | 11.460 | 11.979 | 11.985 | 12.10 (16) |
14 | 12.417 | 12.980 | 12.771 | 13.13 (21) |
15 | 13.375 | 13.980 | 14.09 (26) | |
16 | 14.335 | 14.981 | 15.12 (32) | |
17 | 15.294 | 15.981 | ||
18 | 16.254 | 16.981 | ||
19 | 17.214 | 17.982 | ||
20 | 18.174 | 18.982 | ||
21 | 19.135 | 19.982 | ||
22 | 20.096 | 20.982 | ||
23 | 21.057 | 21.982 | ||
24 | 22.019 | 22.983 | ||
25 | 22.980 | 23.983 | ||
26 | 23.942 | 24.983 | ||
27 | 24.904 | 25.983 | ||
28 | 25.866 | 26.983 | ||
29 | 26.828 | 27.983 | ||
30 | 27.790 | 28.983 | ||
31 | 28.753 | |||
32 | 29.715 | |||
33 | 30.678 | |||
34 | 31.640 | |||
35 | 32.603 | |||
36 | 33.566 | |||
37 | 34.528 | |||
38 | 35.491 | |||
39 | 36.454 | |||
40 | 37.417 | |||
… | ||||
States | Theory | Experiment | ||||
|---|---|---|---|---|---|---|
MAOT | SCUNC | NC | SR | PA |
| |
E | E |
| ||||
4 | 50.7601 | 50.76 | 51.1834 | 50.76 | 50.749 | 0.00 |
5 | 51.8926 | 51.9271 | 52.0367 | 51.926 | 51.928 | 0.03 |
6 | 52.3724 | 52.3847 | 52.4303 | 52.388 | 52.387 | 0.02 |
7 | 52.6159 | 52.6157 | 52.64 | 52.618 | - | 0.00 |
8 | 52.7552 | 52.7485 | 52.7623 | 52.7493 | 52.737 | 0.01 |
9 | 52.8418 | 52.8319 | 52.8394 | 52.832 | 52.827 | 0.01 |
10 | 52.8990 | 52.8876 | 52.8916 | 52.8863 | 52.8863 | 0.01 |
11 | 52.9386 | 52.9266 | 52.9282 | 52.9243 | 0.01 | |
12 | 52.9670 | 52.955 | 52.9549 | 52.9513 | 0.00 | |
13 | 52.9881 | 52.9763 | ||||
14 | 53.0041 | 52.9926 | ||||
15 | 53.0164 | 53.0055 | ||||
16 | 53.0262 | 53.0157 | ||||
17 | 53.0340 | 53.0241 | ||||
18 | 53.0403 | 53.0309 | ||||
19 | 53.0455 | 53.0366 | ||||
20 | 53.0499 | 53.0414 | ||||
21 | 53.0535 | 53.0455 | ||||
22 | 53.0566 | 53.049 | ||||
23 | 53.0592 | 53.052 | ||||
24 | 53.0614 | 53.0547 | ||||
25 | 53.0634 | 53.0569 | ||||
26 | 53.0651 | 53.059 | ||||
27 | 53.0665 | 53.0607 | ||||
28 | 53.0678 | 53.0623 | ||||
29 | 53.0690 | 53.0637 | ||||
30 | 53.0700 | 53.065 | ||||
31 | 53.0709 | |||||
32 | 53.0717 | |||||
33 | 53.0724 | |||||
34 | 53.0731 | |||||
35 | 53.0737 | |||||
36 | 53.0742 | |||||
37 | 53.0747 | |||||
38 | 53.0751 | |||||
39 | 53.0756 | |||||
40 | 53.0759 | |||||
… | ||||||
∞ | 53.082 | |||||
States | Theory | Experiment | ||
|---|---|---|---|---|
MAOT | SCUNC | NC | SR | |
4 | 2.959 | 2.421 | 2.676 | 2.423 (3) |
5 | 3.879 | 3.432 | 3.606 | 3.438(6) |
6 | 4.810 | 4.417 | 4.567 | 4.444(13) |
7 | 5.750 | 5.401 | 5.544 | 5.446 (24) |
8 | 6.695 | 6.388 | 6.580 | 6.443 (15) |
9 | 7.644 | 7.376 | 7.578 | 7.452 (23) |
10 | 8.595 | 8.366 | 8.576 | 8.447 (33) |
11 | 9.548 | 9.357 | 9.576 | 9.440 (5) |
12 | 10.503 | 10.350 | 10.574 | 10.40 (13) |
13 | 11.460 | 11.344 | ||
14 | 12.417 | 12.338 | ||
15 | 13.375 | 13.333 | ||
16 | 14.335 | 14.329 | ||
17 | 15.294 | 15.325 | ||
18 | 16.254 | 16.322 | ||
19 | 17.214 | 17.318 | ||
20 | 18.174 | 18.316 | ||
21 | 19.135 | 19.313 | ||
22 | 20.096 | 20.311 | ||
23 | 21.057 | 21.309 | ||
24 | 22.019 | 22.307 | ||
25 | 22.980 | 23.305 | ||
26 | 23.942 | 24.303 | ||
27 | 24.904 | 25.301 | ||
28 | 25.866 | 26.300 | ||
29 | 26.828 | 27.298 | ||
30 | 27.790 | 28.297 | ||
31 | 28.753 | |||
32 | 29.715 | |||
33 | 30.678 | |||
34 | 31.640 | |||
35 | 32.603 | |||
36 | 33.566 | |||
37 | 34.528 | |||
38 | 35.491 | |||
39 | 36.454 | |||
40 | 37.417 | |||
… | ||||
States | Na+ | Mg2+ | ||||||
|---|---|---|---|---|---|---|---|---|
MAOT | SCUNC | HPTL | DHF | MAOT | SCUNC | DHF | HVSS | |
E | E | |||||||
3 | 69.950 | 69.95 | 69.95 | 73.746 | 98.776 | 98.776 | 101.525 | 98.278 |
4 | 75.320 | 75.32 | 75.18 | 109.004 | 109.004 | 108.722 | ||
5 | 77.372 | 77.365 | 77.17 | 113.072 | 113.057 | 112.888 | ||
6 | 78.364 | 78.359 | 78.14 | 115.089 | 115.078 | - | ||
7 | 78.920 | 78.918 | 78.7 | 116.238 | 116.232 | 116.126 | ||
8 | 79.262 | 79.263 | 79.04 | 116.955 | 116.954 | |||
9 | 79.489 | 79.491 | 117.434 | 117.436 | ||||
10 | 79.648 | 79.65 | 117.771 | 117.773 | ||||
11 | 79.763 | 79.765 | 118.016 | 118.018 | ||||
12 | 79.849 | 79.851 | 118.201 | 118.203 | ||||
13 | 79.915 | 79.917 | 118.343 | 118.344 | ||||
14 | 79.967 | 79.968 | 118.455 | 118.456 | ||||
15 | 80.009 | 80.009 | 118.545 | 118.545 | ||||
16 | 80.043 | 80.043 | 118.618 | 118.617 | ||||
17 | 80.070 | 80.07 | 118.678 | 118.677 | ||||
18 | 80.094 | 80.093 | 118.729 | 118.727 | ||||
19 | 80.113 | 80.112 | 118.771 | 118.769 | ||||
20 | 80.130 | 80.128 | 118.807 | 118.805 | ||||
21 | 80.144 | 80.142 | 118.838 | 118.835 | ||||
22 | 80.156 | 80.154 | 118.864 | 118.862 | ||||
23 | 80.167 | 80.165 | 118.888 | 118.885 | ||||
24 | 80.176 | 80.174 | 118.908 | 118.905 | ||||
25 | 80.184 | 80.182 | 118.926 | 118.922 | ||||
26 | 80.191 | 80.189 | 118.941 | 118.938 | ||||
27 | 80.197 | 80.196 | 118.955 | 118.952 | ||||
28 | 80.203 | 80.201 | 118.968 | 118.964 | ||||
29 | 80.208 | 80.206 | 118.979 | 118.975 | ||||
30 | 80.213 | 80.211 | 118.989 | 118.985 | ||||
31 | 80.217 | 118.998 | ||||||
32 | 80.221 | 119.006 | ||||||
33 | 80.224 | 119.014 | ||||||
34 | 80.227 | 119.020 | ||||||
35 | 80.230 | 119.027 | ||||||
36 | 80.232 | 119.032 | ||||||
37 | 80.235 | 119.038 | ||||||
38 | 80.237 | 119.042 | ||||||
39 | 80.239 | 119.047 | ||||||
40 | 80.241 | 119.051 | ||||||
… | ||||||||
∞ | 80.274 | 80.274 | 80.091 | 83.877 | 119,126 | 119,126 | 122.356 | 118.766 |
n | Na+ | Mg2+ | ||||
|---|---|---|---|---|---|---|
MAOT | SCUNC | DHF | MAOT | SCUNC | DHF | |
Γ | Γ | Γ | Γ | Γ | Γ | |
3 | 51.55 | 51.56 | 60 | 94.53 | 94.51 | 90 |
4 | 22.50 | 22.50 | 43.45 | 43.44 | ||
5 | 12.38 | 12.11 | 24.72 | 24.40 | ||
6 | 7.77 | 7.50 | 15.89 | 15.58 | ||
7 | 5.31 | 5.09 | 11.05 | 10.80 | ||
8 | 3.85 | 3.67 | 8.11 | 7.92 | ||
9 | 2.91 | 2.77 | 6.20 | 6.06 | ||
10 | 2.27 | 2.17 | 4.88 | 4.78 | ||
11 | 1.81 | 1.74 | 3.94 | 3.87 | ||
12 | 1.48 | 1.42 | 3.24 | 3.20 | ||
13 | 1.23 | 1.19 | 2.71 | 2.68 | ||
14 | 1.04 | 1.01 | 2.30 | 2.29 | ||
15 | 0.89 | 0.86 | 1.97 | 1.97 | ||
16 | 0.76 | 1.71 | ||||
17 | 0.67 | 1.50 | ||||
18 | 0.58 | 1.32 | ||||
19 | 0.52 | 1.17 | ||||
20 | 0.46 | 1.05 | ||||
21 | 0.41 | 0.94 | ||||
22 | 0.37 | 0.85 | ||||
23 | 0.34 | 0.77 | ||||
24 | 0.31 | 0.70 | ||||
25 | 0.28 | 0.65 | ||||
26 | 0.26 | 0.59 | ||||
27 | 0.24 | 0.55 | ||||
28 | 0.22 | 0.50 | ||||
29 | 0.20 | 0.47 | ||||
30 | 0.19 | 0.44 | ||||
n | Resonance energies (E, eV) | ||||||
|---|---|---|---|---|---|---|---|
Ep | Ea | Eb | Ec | Ed | Ee |
| |
3 | 889.45 | 889.945 | 890.40 | 890.40 | 890.40 | 890.40 | 0.50 |
4 | 894.90 | 894.90 | 895.00 | 895.40 | 895.40 | 895.40 | 0.00 |
5 | 896.96 | 897.10 | 897.20 | 897.30 | 897.30 | 897.30 | 0.14 |
6 | 897.93 | 897.90 | 898.28 | 899.2 | 899.2 | 899.2 | 0.03 |
7 | 898.46 | ||||||
8 | 898.78 | ||||||
9 | 898.98 | ||||||
10 | 899.12 | ||||||
11 | 899.22 | ||||||
12 | 899.29 | ||||||
13 | 899.35 | ||||||
14 | 899.39 | ||||||
15 | 899.43 | ||||||
16 | 899.45 | ||||||
17 | 899.47 | ||||||
18 | 899.49 | ||||||
19 | 899.51 | ||||||
20 | 899.52 | ||||||
… | …. | ||||||
∞ | 899.63 | 899.63 | |||||
MAOT | Modified Atomic Orbital Theory |
SCUNC | Screening Constant by Unit Nuclear Charge |
DHF | Dirac-Hartree-Fock |
SR | Synchrotron Radiation |
PA | Photoabsorption |
NC | Numerical Calculations |
HPTL | High-power Adjustable Laser |
HVSS | High-voltage Spark Spectra |
DES | Doubly Excited States |
| [1] | A. Müller, D. Bernhardt, A. Borovik Jr., T. Buhr, J. Hellhund, K. Holste, A. L. D. Kilcoyne, S. Klumpp, M. Martins, S. Ricz, Astrophys. J. 836, 166 (2017), |
| [2] | Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481, |
| [3] | I. Sakho, At. Data. Nuc. Data Tables 108, 57 (2016), |
| [4] | Sultana N. Nahar, New Astronomy 67 (2019)97-102, |
| [5] | Rubin, R. H., 2004. Proc. IAU Symp. 217. In: Duc, P. A., Braine, J., Brinks, E. (Eds.), Recycling Intergalactic and Interstellar Matter. Astron. Soc. Pac. pp. 190. San Francisco. |
| [6] | Rubin, R. H., Dufour, R. J., Geballe, T. R., Colgan, S. W. J., Harrington, J. P., Lord, S. D., Liao, A. L., Levine, D. A., 2001. ASP Conf. Ser. In: Ferland, G., Savin, W. D. (Eds.), Spectroscopic Challenges of Photoionized Plasmas. Astron. Soc. Pac. Vol. 247. pp. 479. San Francisco. |
| [7] | Dance, D., Palay, E., Nahar, S. N., Pradhan, A. K., 2013. MNRAS 435, 1576–1581. TOPbase. The Opacity Project database: |
| [8] | Crockett, N. R., Garnett, D. R., Massey, P., Jacoby, G., 2006. ApJ 637, 741–751. |
| [9] | S. B. Whitfield, R. Wehlitz, H. R. Varma, T. Banerjee, P. C. Deshmukh, and S. T. Manson, J. Phys. B 39, L335 (2006). |
| [10] | A. K. S. Jha, P. Jha, S. Tyagi, and M. Mohan, Eur. Phys. J. D 39, 391 (2006). |
| [11] | K. Schulz, M. Domke, R. Püttner, A. Gutiérrez, G. Kaindl, G. Miecznik and C. H. Greene, Phys. Rev. A 54, 3095 (1996), |
| [12] | A. Diallo, M. Diouldé Ba, J. K. Badiane, M. T. Gning, M. Sow and I. Sakho, Jour. Mod. Phys. 9, 2594 (2018), |
| [13] | A. Diallo, M. D. Ba, J. K. Badiane, M. T. Gning, M. Sow and I. Sakho, Jour. Atom, Mol. Conden. Nano Phys. 5, 215 (2018), |
| [14] | T. B. Lucatorto and T. J. Mcllrath, Phys. Rev. Lett. 37, 428 (1976). |
| [15] | K. Codling, R. P. Madden, D. L. Ederer, Phys. Rev. 155 (1967) 26. |
| [16] | M. Nrisimhamurty, G. Aravind, P. C. Deshmukh, S. T. Manson, Phys. Rev. A 91 (2015) 013404. |
| [17] | S. O. Kastner, A. M. Crooker, W. E. Behring, and L. Cohen, Phys. Rev. A 16, 577 (1977). |
| [18] | Witthoeft, M. C., Bautista, M. A., Mendoza, C., et al. 2009, Astrophys. J., 182, 127 |
| [19] | Gorczyca, T. W. 2000, Phys. Rev. A, 61, 024702, |
| [20] | Juett, A. M., Schulz, N. S., Chakrabarty, D., & Gorczyca, T. W. 2006, Astrophys. J, 648, 1066. |
| [21] | Gatuzz, E., García, J., Kallman, T., Mendoza, C., & Gorczyca, T. 2015, Astrophys. J, 800, 29. |
APA Style
Diallo, A., Badiane, J. K., Millimono, T. N., Sakouvogui, A., Ba, M. D. (2025). Calculations of Resonances Energies of the Ne Atom, Ne-like Na+, Mg2+, and Ne+ Ions, Framework of the Modified Atomic Orbital Theory. Nuclear Science, 10(1), 1-14. https://doi.org/10.11648/j.ns.20251001.11
ACS Style
Diallo, A.; Badiane, J. K.; Millimono, T. N.; Sakouvogui, A.; Ba, M. D. Calculations of Resonances Energies of the Ne Atom, Ne-like Na+, Mg2+, and Ne+ Ions, Framework of the Modified Atomic Orbital Theory. Nucl. Sci. 2025, 10(1), 1-14. doi: 10.11648/j.ns.20251001.11
@article{10.11648/j.ns.20251001.11,
author = {Abdourahmane Diallo and Jean Kouhissoré Badiane and Tamba Nicolas Millimono and Ansoumane Sakouvogui and Mamadou Dioulde Ba},
title = {Calculations of Resonances Energies of the Ne Atom, Ne-like Na+, Mg2+, and Ne+ Ions, Framework of the Modified Atomic Orbital Theory},
journal = {Nuclear Science},
volume = {10},
number = {1},
pages = {1-14},
doi = {10.11648/j.ns.20251001.11},
url = {https://doi.org/10.11648/j.ns.20251001.11},
eprint = {https://article.sciencepublishinggroup.com/pdf/10.11648.j.ns.20251001.11},
abstract = {In the literature, there are several theoretical and experimental methods for calculating the resonance energies and natural widths of atomic systems. For the 1s22s2p6np ¹P1 series of Ne, Na+, Mg2+, and the 1s2s22p5np ¹P1 series of Ne+, various methods have been employed. In this present work, resonance energies resonance energies and width of the 1s22s2p6 np 1P1 series of the Ne, Na+, Mg2+, and 1s2s22p5 np 1P1 of Ne+ ions are calculated. The energies are calculated in the framework of the Modified Atomic Orbital Theory (MAOT). The results obtained compared very well with theoretical and experimental literature values. The possibility to use the MOAT formalism report rapidly with an excellent accuracy the position of the resonances as well as their width within simple analytical formulae is demonstrated. It is demonstrated that the MOAT-method can be used to assist fruitfully experiments for identifying narrow resonance energies. Thus, our results can be used as reference data for the interpretation of atomic spectra for the diagnosis of astrophysical and laboratory plasma. Through this method new values of these energies are reported going up to n=40. These excellent agreements between theory and experiments indicate that the MAOT formalism can be used to report accurate high-lying excited Rydberg series of atomic species for the diagnostic and the modeling of astrophysical or laboratory plasmas.},
year = {2025}
}
TY - JOUR T1 - Calculations of Resonances Energies of the Ne Atom, Ne-like Na+, Mg2+, and Ne+ Ions, Framework of the Modified Atomic Orbital Theory AU - Abdourahmane Diallo AU - Jean Kouhissoré Badiane AU - Tamba Nicolas Millimono AU - Ansoumane Sakouvogui AU - Mamadou Dioulde Ba Y1 - 2025/02/11 PY - 2025 N1 - https://doi.org/10.11648/j.ns.20251001.11 DO - 10.11648/j.ns.20251001.11 T2 - Nuclear Science JF - Nuclear Science JO - Nuclear Science SP - 1 EP - 14 PB - Science Publishing Group SN - 2640-4346 UR - https://doi.org/10.11648/j.ns.20251001.11 AB - In the literature, there are several theoretical and experimental methods for calculating the resonance energies and natural widths of atomic systems. For the 1s22s2p6np ¹P1 series of Ne, Na+, Mg2+, and the 1s2s22p5np ¹P1 series of Ne+, various methods have been employed. In this present work, resonance energies resonance energies and width of the 1s22s2p6 np 1P1 series of the Ne, Na+, Mg2+, and 1s2s22p5 np 1P1 of Ne+ ions are calculated. The energies are calculated in the framework of the Modified Atomic Orbital Theory (MAOT). The results obtained compared very well with theoretical and experimental literature values. The possibility to use the MOAT formalism report rapidly with an excellent accuracy the position of the resonances as well as their width within simple analytical formulae is demonstrated. It is demonstrated that the MOAT-method can be used to assist fruitfully experiments for identifying narrow resonance energies. Thus, our results can be used as reference data for the interpretation of atomic spectra for the diagnosis of astrophysical and laboratory plasma. Through this method new values of these energies are reported going up to n=40. These excellent agreements between theory and experiments indicate that the MAOT formalism can be used to report accurate high-lying excited Rydberg series of atomic species for the diagnostic and the modeling of astrophysical or laboratory plasmas. VL - 10 IS - 1 ER -